Salinan Soal Matematika Seleksi SMA DEL 2020
Sunday, 9 August 2020
Add Comment
Selamat Siang
Kemarin, saat pembelajaran di sekolah, ada masuk chat di WA dari nomor tidak dikenal
Mengirimkan soal - soal ini
Katanya soal seleksi DEL
Karena saya tidak kenal nomornya, saya abaikan saja
Toh saya juga sedang mengajar
Setelah selesai pembelajaran, saya melihat soal - soalnya
Ternyata soal sejenis Olimpiade
Saya tidak tahu, apakah ada seleksi di DEL pada 08 Agustus 2020
Saya googling, ternyata PSB di SMA DEL sudah selesai April lalu
Jadi soal apakah?
Apapun itu, saya akan membagikan soalnya
Soalnya sudah saya edit, sehingga bukan soal asli.
Semoga bermanfaat bagi yang belajar olimpiade.
Beberapa soal, sudah disertakan solusi
Semangat
Soal Seleksi SMA DEL 2020
1. Diberikan segitiga lancip PQR. Misalkan garis singgung lingkaran luar segitiga tersebut di titik Q dan R berpotongan di S. Titik X dan Y dibuat pada garis PQ dan PR, berturut – turut, sehingga ∠SXP = ∠SYP = 90 derajat. Misalkan M adalah titik tengan ruas garis QR.
a. Buktikan bahwa QXSM dan RYSM keduanya merupakan segiempat tali busur (dengan kata lain, QXDM terletak di satu lingkaran, begitu juga RYSM)
b. Buktikan bahwa M adalah titik tinggi segitiga PXY (dengan kata lain, PM tegak lurus terhadap XY, XM tegak lurus terhadap PY, dan YM tegak lurus terhadap PX)
2. Suzy adalah seorang artis korea selatan yang terkenal. Ia akan melakukan tur selama 8 hari di kota P, Q, R, dan S. Setiap harinya, Suzy akan melakukan 1 konser di kota tertentu, dan akan berpindah ke kota lain untuk konser (seperti dalam gambar). Diketahui bahwa semua kota terhubung dengan kota lainnya, kecuali kota P dan R. Tentukan banyaknya kemungkinan rute tur yang berawal di kota P dan berakhir di kota P pula.
3. Untuk semua bilangan asli n, misalkan t(n) menyatakan banyaknya bilangan asli yang habis membagi n. Sebagai contoh, jika n = 42, maka t(n) = 8. Jika n memiliki bentuk aritmatika

dengan p1, p2, ..., pk merupakan bilangan prima berbeda dan a1, a2, ..., ak merupakan bilangan asli, dapat ditunjukkan bahwa t(n) = (a1 + 1)(a2 + 1)...(ak + 1).
Tentukan jumlah semua bilangan asli n yang memenuhi persamaan: t(n) = 3 dan t(n + 152) = 9
4. Tentukan nilai dari 16a + 25b + 36c + 49d + 64e, jika diberikan sistem persamaan:
a + 4b + 9c + 16d + 25e = 4
4a + 9b + 16c + 25d + 36e = 5
9a + 16b + 25c + 36d + 49e = 6
5. Tentukan banyaknya tripel bilangan asli (x, y, z) sedemikian sehingga
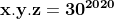
dan memenuhi:

Demikianlah soal Matematika Seleksi SMA DEL 2020
Semoga Bermanfaat.
Kemarin, saat pembelajaran di sekolah, ada masuk chat di WA dari nomor tidak dikenal
Mengirimkan soal - soal ini
Katanya soal seleksi DEL
Karena saya tidak kenal nomornya, saya abaikan saja
Toh saya juga sedang mengajar
Setelah selesai pembelajaran, saya melihat soal - soalnya
Ternyata soal sejenis Olimpiade
Saya tidak tahu, apakah ada seleksi di DEL pada 08 Agustus 2020
Saya googling, ternyata PSB di SMA DEL sudah selesai April lalu
Jadi soal apakah?
Apapun itu, saya akan membagikan soalnya
Soalnya sudah saya edit, sehingga bukan soal asli.
Semoga bermanfaat bagi yang belajar olimpiade.
Beberapa soal, sudah disertakan solusi
Semangat
Soal Seleksi SMA DEL 2020
1. Diberikan segitiga lancip PQR. Misalkan garis singgung lingkaran luar segitiga tersebut di titik Q dan R berpotongan di S. Titik X dan Y dibuat pada garis PQ dan PR, berturut – turut, sehingga ∠SXP = ∠SYP = 90 derajat. Misalkan M adalah titik tengan ruas garis QR.
a. Buktikan bahwa QXSM dan RYSM keduanya merupakan segiempat tali busur (dengan kata lain, QXDM terletak di satu lingkaran, begitu juga RYSM)
b. Buktikan bahwa M adalah titik tinggi segitiga PXY (dengan kata lain, PM tegak lurus terhadap XY, XM tegak lurus terhadap PY, dan YM tegak lurus terhadap PX)
2. Suzy adalah seorang artis korea selatan yang terkenal. Ia akan melakukan tur selama 8 hari di kota P, Q, R, dan S. Setiap harinya, Suzy akan melakukan 1 konser di kota tertentu, dan akan berpindah ke kota lain untuk konser (seperti dalam gambar). Diketahui bahwa semua kota terhubung dengan kota lainnya, kecuali kota P dan R. Tentukan banyaknya kemungkinan rute tur yang berawal di kota P dan berakhir di kota P pula.
3. Untuk semua bilangan asli n, misalkan t(n) menyatakan banyaknya bilangan asli yang habis membagi n. Sebagai contoh, jika n = 42, maka t(n) = 8. Jika n memiliki bentuk aritmatika
dengan p1, p2, ..., pk merupakan bilangan prima berbeda dan a1, a2, ..., ak merupakan bilangan asli, dapat ditunjukkan bahwa t(n) = (a1 + 1)(a2 + 1)...(ak + 1).
Tentukan jumlah semua bilangan asli n yang memenuhi persamaan: t(n) = 3 dan t(n + 152) = 9
4. Tentukan nilai dari 16a + 25b + 36c + 49d + 64e, jika diberikan sistem persamaan:
a + 4b + 9c + 16d + 25e = 4
4a + 9b + 16c + 25d + 36e = 5
9a + 16b + 25c + 36d + 49e = 6
5. Tentukan banyaknya tripel bilangan asli (x, y, z) sedemikian sehingga
dan memenuhi:
Demikianlah soal Matematika Seleksi SMA DEL 2020
Semoga Bermanfaat.


0 Response to "Salinan Soal Matematika Seleksi SMA DEL 2020"
Post a Comment